1. 动力学建模

四旋翼无人机的非线性动力学模型的建模方式为：

平移运动：描述无人机在 X、Y、Z 方向上的运动。
旋转运动：描述无人机的姿态（俯仰角、横滚角、偏航角）。
控制输入：四个电机的转速与无人机的升力和力矩之间的关系。

动力学模型的核心公式如下：

1.1 平移动力学：

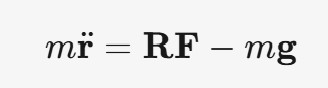
其中，m是无人机质量（标量值，它反映了无人机的惯性大小），r¨是位置向量r对时间的二阶导数（也就是加速度向量），R是旋转矩阵（将机体坐标系中的力转换到惯性坐标系），F是升力向量，g是重力加速度。

左边 mr¨ 表示无人机的惯性力，即质量乘以加速度。右边 RF 表示无人机产生的升力在全局坐标系中的投影，因为升力 F 通常是在无人机的机体坐标系下定义的，而描述无人机的运动一般是在惯性坐标系下进行的，所以需要用旋转矩阵 R 对升力向量 F 进行坐标转换。mg 表示重力对无人机的影响。

该公式描述了无人机在全局坐标系中的运动（即无人机在惯性坐标系中的合力），由升力和重力共同决定。通过控制升力 F 和旋转矩阵 R，可以调节无人机的位置和速度。

2.2 旋转动力学

其中，I是无人机的惯性矩阵（在机体坐标系中，描述了无人机对旋转的抵抗能力），ω˙是无人机的角加速度向量，ω是无人机的角速度向量（在机体坐标系中），M是作用在无人机上的力矩向量（在机体坐标系中）。

左边 Iω˙ 表示角加速度引起的惯性力矩，类似于平动中的 ma。ω×Iω 表示科里奥利力矩，是由于旋转引起的非线性效应，因为无人机在旋转过程中，不同部分的质量具有不同的线速度和角速度，从而产生的一种附加力矩，它反映了旋转运动中的耦合效应。右边 M 表示外部力矩（如电机产生的力矩）。

该公式描述了无人机的旋转运动，由外部力矩和惯性效应共同决定，即无人机的角动量变化率等于作用在无人机上的外力矩。通过控制力矩 M，可以调节无人机的姿态（如滚转、俯仰和偏航）。

2. PID控制算法

PID控制算法 是一种经典的反馈控制算法，广泛应用于工业控制、机器人、航空航天等领域。PID是 比例（Proportional）、积分（Integral）、微分（Derivative） 的缩写，通过调节这三个参数，控制器可以对系统的误差进行调节，使系统输出尽可能接近目标值。

2.1 算法

PID控制器的输出由三部分组成：

其中：

u(t)：控制器的输出。
e(t)：误差，即目标值（setpoint）与当前值（measured value）的差。
K_p：比例增益，控制当前误差的权重。
K_i：积分增益，控制累积误差的权重。
K_d：微分增益，控制误差变化率的权重。

PID的三个部分解释：

1. 比例项（P）

作用：根据当前误差的大小，直接产生控制输出。
特点：
- 误差越大，输出越大。
- 比例项可以快速减小误差，但可能导致系统振荡或稳态误差。

2. 积分项（I）

作用：累积历史误差，消除稳态误差。
特点：
- 积分项可以消除系统的稳态误差（如温度控制中的恒定偏差）。
- 但积分项过大会导致系统响应变慢或超调。

3. 微分项（D）

作用：根据误差的变化率，预测未来的误差趋势，抑制系统的振荡。
特点：
- 微分项可以提高系统的稳定性，减少超调。
- 但对噪声敏感，可能放大高频噪声。

2.2 实现代码

在实际应用中，PID控制器通常以离散形式实现。离散化公式如下：

其中：

u(k)：第 k 时刻的控制输出。
e(k)：第 k 时刻的误差。
Δt：时间步长。

以下是一个简单的四旋翼无人机 PID 控制算法的 Python 实现示例：

class PIDController:
    def __init__(self, kp, ki, kd):
        # PID控制器通过调节比例（P）、积分（I）和微分（D）三个参数，实现对系统误差的调节。
        self.kp = kp  # 比例增益，控制当前误差的权重
        self.ki = ki  # 积分增益，控制累积误差的权重。
        self.kd = kd  # 微分增益，控制误差变化率的权重。
        self.prev_error = 0  # 上一次的误差值，用于计算微分项。
        self.integral = 0  # 累积误差值，用于计算积分项。

    def compute(self, setpoint, measured_value, dt):  # setpoint：目标值（期望值），measured_value：当前测量值，dt：时间步长（用于计算积分和微分项）。
        # 根据当前误差、累积误差和误差变化率，计算PID控制器的输出。
        error = setpoint - measured_value  # 计算误差
        self.integral += error * dt  # 计算积分项
        derivative = (error - self.prev_error) / dt  # 计算微分项
        output = self.kp * error + self.ki * self.integral + self.kd * derivative  # 计算PID输出
        self.prev_error = error  # 更新上一次的误差值
        return output

# 姿态控制
pid_roll = PIDController(kp=1.0, ki=0.01, kd=0.1)
roll_setpoint = 0  # 目标横滚角
measured_roll = 0.1  # 当前横滚角
dt = 0.01  # 时间步长
control_output = pid_roll.compute(roll_setpoint, measured_roll, dt)
print("Control Output:", control_output)

计算过程为：

计算误差：error=0−0.1=−0.1
计算积分项：integral=0+(−0.1)×0.01=−0.001
计算微分项：derivative=(−0.1−0) / −0.01=−10
计算PID输出：output=1.0×(−0.1)+0.01×(−0.001)+0.1×(−10)=−0.1−0.0001−1.0=−1.1001
更新上一次的误差值：prev_error=−0.1

输出结果为：

2.3 控制框架

基于 PID 控制 的分层控制框架：

姿态控制：通过调节电机的转速实现无人机的姿态稳定。
控制目标：使无人机的姿态角（俯仰角、横滚角、偏航角）跟踪给定值。
控制输入：电机的转速。
位置控制：在姿态控制的基础上，实现无人机在三维空间中的位置控制。
控制目标：使无人机的位置（X、Y、Z）跟踪给定值。
控制输入：姿态控制器的参考输入。
鲁棒性分析：讨论了控制算法对参数不确定性和外部干扰的鲁棒性。